📓 Cabinet of Ideas

List of Unsolved Problems in Physics Wikipedia

List of unsolved problems in physics - Wikipedia #

Excerpt #

From Wikipedia, the free encyclopedia

From Wikipedia, the free encyclopedia

The following is a list of notable unsolved problems grouped into broad areas of physics.[1]

Some of the major unsolved problems in physics are theoretical, meaning that existing theories seem incapable of explaining a certain observed phenomenon or experimental result. The others are experimental, meaning that there is a difficulty in creating an experiment to test a proposed theory or investigate a phenomenon in greater detail.

There are still some questions beyond the Standard Model of physics, such as the strong CP problem, neutrino mass, matter–antimatter asymmetry, and the nature of dark matter and dark energy.[2][3] Another problem lies within the mathematical framework of the Standard Model itself—the Standard Model is inconsistent with that of general relativity, to the point that one or both theories break down under certain conditions (for example within known spacetime singularities like the Big Bang and the centres of black holes beyond the event horizon).[4]

  • Theory of everything: Is there a singular, all-encompassing, coherent theoretical framework of physics that fully explains and links together all physical aspects of the universe?

  • Dimensionless physical constants: At the present time, the values of various dimensionless physical constants cannot be calculated; they can be determined only by physical measurement.[5][6] What is the minimum number of dimensionless physical constants from which all other dimensionless physical constants can be derived? Are dimensional physical constants necessary at all?

  • Quantum gravity: Can quantum mechanics and general relativity be realized as a fully consistent theory (perhaps as a quantum field theory)?[7] Is spacetime fundamentally continuous or discrete? Would a consistent theory involve a force mediated by a hypothetical graviton, or be a product of a discrete structure of spacetime itself (as in loop quantum gravity)? Are there deviations from the predictions of general relativity at very small or very large scales or in other extreme circumstances that flow from a quantum gravity mechanism?

  • Black holes, black hole information paradox, and black hole radiation: Do black holes produce thermal radiation, as expected on theoretical grounds?[8] Does this radiation contain information about their inner structure, as suggested by gauge–gravity duality, or not, as implied by Hawking’s original calculation? If not, and black holes can evaporate away, what happens to the information stored in them (since quantum mechanics does not provide for the destruction of information)? Or does the radiation stop at some point, leaving black hole remnants? Is there another way to probe their internal structure somehow, if such a structure even exists?

  • The cosmic censorship hypothesis and the chronology protection conjecture: Can singularities not hidden behind an event horizon, known as “ naked singularities”, arise from realistic initial conditions, or is it possible to prove some version of the “cosmic censorship hypothesis” of Roger Penrose which proposes that this is impossible?[9] Similarly, will the closed timelike curves which arise in some solutions to the equations of general relativity (and which imply the possibility of backwards time travel) be ruled out by a theory of quantum gravity which unites general relativity with quantum mechanics, as suggested by the “chronology protection conjecture” of Stephen Hawking?

  • Holographic principle: Is it true that quantum gravity admits a lower-dimensional description that does not contain gravity? A well-understood example of holography is the AdS/CFT correspondence in string theory. Similarly, can quantum gravity in a de Sitter space be understood using dS/CFT correspondence? Can the AdS/CFT correspondence be vastly generalized to the gauge–gravity duality for arbitrary asymptotic spacetime backgrounds? Are there other theories of quantum gravity other than string theory that admit a holographic description?

  • Quantum spacetime or the emergence of spacetime: Is the nature of spacetime at the Planck scale very different from the continuous classical dynamical spacetime that exists in General relativity? In loop quantum gravity, the spacetime is postulated to be discrete from the beginning. In string theory, although originally spacetime was considered just like in General relativity (with the only difference being supersymmetry), recent research building upon the Ryu–Takayanagi conjecture has taught that spacetime in string theory is emergent by using quantum information theoretic concepts such as entanglement entropy in the AdS/CFT correspondence.[10] However, how exactly the familiar classical spacetime emerges within string theory or the AdS/CFT correspondence is still not well understood.

  • Problem of time: In quantum mechanics, time is a classical background parameter, and the flow of time is universal and absolute. In general relativity, time is one component of four-dimensional spacetime, and the flow of time changes depending on the curvature of spacetime and the spacetime trajectory of the observer. How can these two concepts of time be reconciled?[11]

  • Yang–Mills theory: Given an arbitrary compact gauge group, does a non-trivial quantum Yang–Mills theory with a finite mass gap exist? (This problem is also listed as one of the Millennium Prize Problems in mathematics.)[12]

  • Quantum field theory (this is a generalization of the previous problem): Is it possible to construct, in a mathematically rigorous way, a quantum field theory in 4-dimensional spacetime that includes interactions and does not resort to perturbative methods?

Cosmology and general relativity #

[ edit]

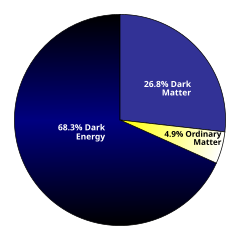
Estimated distribution of dark matter and dark energy in the universe

High-energy/particle physics #

[ edit]

Colour Confinement is the observed phenomenon that colored particles (quarks and gluons) cannot be isolated and are always bound to color neutral groups (at low energies). Such bound states are generally called hadrons.

  • The QCD vacuum: Many of the equations in non-perturbative QCD are currently unsolved. These energies are the energies sufficient for the formation and description of atomic nuclei. How thus does low energy /non-pertubative QCD give rise to the formation of complex nuclei and nuclear constituents?[citation needed]
  • Generations of matter: Why are there three generations of quarks and leptons? Is there a theory that can explain the masses of particular quarks and leptons in particular generations from first principles (a theory of Yukawa couplings)?[31]
  • Neutrino mass: What is the mass of neutrinos, whether they follow Dirac or Majorana statistics? Is the mass hierarchy normal or inverted? Is the CP violating phase equal to 0?[32][33]
  • Reactor antineutrino anomaly: There is an anomaly in the existing body of data regarding the antineutrino flux from nuclear reactors around the world. Measured values of this flux appears to be only 94% of the value expected from theory.[34] It is unknown whether this is due to unknown physics (such as sterile neutrinos), experimental error in the measurements, or errors in the theoretical flux calculations.[35]
  • Strong CP problem and axions: Why is the strong nuclear interaction invariant to parity and charge conjugation? Is Peccei–Quinn theory the solution to this problem? Could axions be the main component of dark matter?
  • Anomalous magnetic dipole moment: Why is the experimentally measured value of the muon’s anomalous magnetic dipole moment (“muon g − 2”) significantly different from the theoretically predicted value of that physical constant?[36]
  • Proton radius puzzle: What is the electric charge radius of the proton? How does it differ from a gluonic charge?
  • Pentaquarks and other exotic hadrons: What combinations of quarks are possible? Why were pentaquarks so difficult to discover?[37] Are they a tightly bound system of five elementary particles, or a more weakly-bound pairing of a baryon and a meson?[38]
  • Mu problem: A problem in supersymmetric theories, concerned with understanding the reasons for parameter values of the theory.
  • Koide formula: An aspect of the problem of particle generations. The sum of the masses of the three charged leptons, divided by the square of the sum of the roots of these masses, to within one standard deviation of observations, is Q = 2⁄3. It is unknown how such a simple value comes about, and why it is the exact arithmetic average of the possible extreme values of ⁠ 1 /3⁠ (equal masses) and 1 (one mass dominates).
  • Strange Matter: Does Strange Matter exist? Is it stable? Can they form Strange Stars? Is strange matter stable at 0 pressure (i.e in the vacuum)?
  • Glueballs: Do they exist in nature?
  • The gallium anomaly: The measurements of the charged-current capture rate of neutrinos on Ga from strong radioactive sources have yielded results below those expected, based on the known strength of the principal transition supplemented by theory.[39]

Astronomy and astrophysics #

[ edit]

  • Solar cycle: How does the Sun generate its periodically reversing large-scale magnetic field? How do other solar-like stars generate their magnetic fields, and what are the similarities and differences between stellar activity cycles and that of the Sun?[40] What caused the Maunder Minimum and other grand minima, and how does the solar cycle recover from a minima state?

  • Coronal heating problem: Why is the Sun’s corona (atmosphere layer) so much hotter than the Sun’s surface? Why is the magnetic reconnection effect many orders of magnitude faster than predicted by standard models?

  • Astrophysical jet: Why do only certain accretion discs surrounding certain astronomical objects emit relativistic jets along their polar axes? Why are there quasi-periodic oscillations in many accretion discs?[41] Why does the period of these oscillations scale as the inverse of the mass of the central object?[42] Why are there sometimes overtones, and why do these appear at different frequency ratios in different objects?[43]

  • Diffuse interstellar bands: What is responsible for the numerous interstellar absorption lines detected in astronomical spectra? Are they molecular in origin, and if so which molecules are responsible for them? How do they form?[44][45]

  • Supermassive black holes: What is the origin of the M–sigma relation between supermassive black hole mass and galaxy velocity dispersion?[46] How did the most distant quasars grow their supermassive black holes up to 1010 solar masses so early in the history of the universe?

  • Kuiper cliff: Why does the number of objects in the Solar System’s Kuiper belt fall off rapidly and unexpectedly beyond a radius of 50 astronomical units?

  • Flyby anomaly: Why is the observed energy of satellites flying by planetary bodies sometimes different by a minute amount from the value predicted by theory?

  • Galaxy rotation problem: Is dark matter responsible for differences in observed and theoretical speed of stars revolving around the centre of galaxies, or is it something else?

    Rotation curve of a typical spiral galaxy: predicted (A) and observed (B). Can the discrepancy between the curves be attributed to dark matter?

  • Supernovae: What is the exact mechanism by which an implosion of a dying star becomes an explosion?

  • p-nuclei: What astrophysical process is responsible for the nucleogenesis of these rare isotopes?

  • Ultra-high-energy cosmic ray:[17] Why is it that some cosmic rays appear to possess energies that are impossibly high, given that there are no sufficiently energetic cosmic ray sources near the Earth? Why is it that (apparently) some cosmic rays emitted by distant sources have energies above the Greisen–Zatsepin–Kuzmin limit?[47][17]

  • Rotation rate of Saturn: Why does the magnetosphere of Saturn exhibit a (slowly changing) periodicity close to that at which the planet’s clouds rotate? What is the true rotation rate of Saturn’s deep interior?[48]

  • Origin of magnetar magnetic field: What is the origin of magnetar magnetic field?

  • Large-scale anisotropy: Is the universe at very large scales anisotropic, making the cosmological principle an invalid assumption? The number count and intensity dipole anisotropy in radio, NRAO VLA Sky Survey (NVSS) catalogue[49] is inconsistent with the local motion as derived from cosmic microwave background[50][51] and indicate an intrinsic dipole anisotropy. The same NVSS radio data also shows an intrinsic dipole in polarization density and degree of polarization[52] in the same direction as in number count and intensity. There are several other observations revealing large-scale anisotropy. The optical polarization from quasars shows polarization alignment over a very large scale of Gpc.[53][54][55] The cosmic-microwave-background data shows several features of anisotropy,[56][57][58][59] which are not consistent with the Big Bang model.

  • Age–metallicity relation in the Galactic disk: Is there a universal age–metallicity relation (AMR) in the Galactic disk (both “thin” and “thick” parts of the disk)? Although in the local (primarily thin) disk of the Milky Way there is no evidence of a strong AMR,[60] a sample of 229 nearby “thick” disk stars has been used to investigate the existence of an age–metallicity relation in the Galactic thick disk, and indicate that there is an age–metallicity relation present in the thick disk.[61][62] Stellar ages from asteroseismology confirm the lack of any strong age–metallicity relation in the Galactic disc.[63]

  • The lithium problem: Why is there a discrepancy between the amount of lithium-7 predicted to be produced in Big Bang nucleosynthesis and the amount observed in very old stars?[64]

  • Ultraluminous X-ray sources (ULXs): What powers X-ray sources that are not associated with active galactic nuclei but exceed the Eddington limit of a neutron star or stellar black hole? Are they due to intermediate-mass black holes? Some ULXs are periodic, suggesting non-isotropic emission from a neutron star. Does this apply to all ULXs? How could such a system form and remain stable?

  • Fast radio bursts (FRBs): What causes these transient radio pulses from distant galaxies, lasting only a few milliseconds each? Why do some FRBs repeat at unpredictable intervals, but most do not? Dozens of models have been proposed, but none have been widely accepted.[65]

The “ island of stability” in the proton vs. neutron number plot for heavy nuclei

Condensed matter physics #

[ edit]

A sample of a cuprate superconductor (specifically BSCCO). The mechanism for superconductivity of these materials is unknown.

Magnetoresistance in a u = 8/5 fractional quantum Hall state

Quantum computing and quantum information #

[ edit]

  • Threshold problem: Can we go beyond the noisy intermediate-scale quantum era? Can quantum computers reach fault tolerance? Is it possible to have enough qubit scalability to implement quantum error correction? What is the most promising candidate platforms to physically implement qubits?[89]

  • Topological qubits: Topological quantum computers are promising but can they be built? Can we demonstrate Majorana zero modes conclusively?[90]

  • Temperature: Can quantum computing be performed at non-cryogenic temperatures? Can we build room temperature quantum computers?[91]

  • Complexity classes problems: What is the relation of BQP and BPP? What is the relation between BQP and NP? Can computation in plausible physical theories (quantum algorithms) go beyond BQP?[89]

  • Post-quantum cryptography: Can we prove that some cryptographic protocols are safe against quantum computers?[89]

  • Quantum capacity: The capacity of a quantum channel is in general not known.[92]

  • Plasma physics and fusion power: Fusion energy may potentially provide power from an abundant resource (e.g. hydrogen) without the type of radioactive waste that fission energy currently produces. However, can ionized gases (plasma) be confined long enough and at a high enough temperature to create fusion power? What is the physical origin of H-mode?[93]

  • The injection problem: Fermi acceleration is thought to be the primary mechanism that accelerates astrophysical particles to high energy. However, it is unclear what mechanism causes those particles to initially have energies high enough for Fermi acceleration to work on them.[94]

  • AlfvĂ©nic turbulence: In the solar wind and the turbulence in solar flares, coronal mass ejections, and magnetospheric substorms are major unsolved problems in space plasma physics.[95]

  • Stochasticity and robustness to noise in gene expression: How do genes govern our body, withstanding different external pressures and internal stochasticity? Certain models exist for genetic processes, but we are far from understanding the whole picture, in particular in development where gene expression must be tightly regulated.

  • Quantitative study of the immune system: What are the quantitative properties of immune responses? What are the basic building blocks of immune system networks?

  • Homochirality: What is the origin of the preponderance of specific enantiomers in biochemical systems?

  • Magnetoreception: How do animals (e.g. migratory birds) sense the Earth’s magnetic field?

  • Protein structure prediction: How is the three-dimensional structure of proteins determined by the one-dimensional amino acid sequence? How can proteins fold on microsecond to second timescales when the number of possible conformations is astronomical and conformational transitions occur on the picosecond to microsecond timescale? Can algorithms be written to predict a protein’s three-dimensional structure from its sequence? Do the native structures of most naturally occurring proteins coincide with the global minimum of the free energy in conformational space? Or are most native conformations thermodynamically unstable, but kinetically trapped in metastable states? What keeps the high density of proteins present inside cells from precipitating?[96]

  • Quantum biology: Can coherence be maintained in biological systems at timeframes long enough to be functionally important? Are there non-trivial aspects of biology or biochemistry that can only be explained by the persistence of coherence as a mechanism?

Foundations of physics #

[ edit]

  • Interpretation of quantum mechanics: How does the quantum description of reality, which includes elements such as the superposition of states and wavefunction collapse or quantum decoherence, give rise to the reality we perceive?[47] Another way of stating this question regards the measurement problem: What constitutes a “measurement” which apparently causes the wave function to collapse into a definite state? Unlike classical physical processes, some quantum mechanical processes (such as quantum teleportation arising from quantum entanglement) cannot be simultaneously “local”, “causal”, and “real”, but it is not obvious which of these properties must be sacrificed,[97] or if an attempt to describe quantum mechanical processes in these senses is a category error such that a proper understanding of quantum mechanics would render the question meaningless. Can the many worlds interpretation resolve it?
  • Arrow of time (e.g. entropy’s arrow of time): Why does time have a direction? Why did the universe have such low entropy in the past, and time correlates with the universal (but not local) increase in entropy, from the past and to the future, according to the second law of thermodynamics?[47] Why are CP violations observed in certain weak force decays, but not elsewhere? Are CP violations somehow a product of the second law of thermodynamics, or are they a separate arrow of time? Are there exceptions to the principle of causality? Is there a single possible past? Is the present moment physically distinct from the past and future, or is it merely an emergent property of consciousness? What links the quantum arrow of time to the thermodynamic arrow?
  • Locality: Are there non-local phenomena in quantum physics?[98][99] If they exist, are non-local phenomena limited to the entanglement revealed in the violations of the Bell inequalities, or can information and conserved quantities also move in a non-local way? Under what circumstances are non-local phenomena observed? What does the existence or absence of non-local phenomena imply about the fundamental structure of spacetime? How does this elucidate the proper interpretation of the fundamental nature of quantum physics?
  • Quantum mind: Do quantum mechanical phenomena, such as entanglement and superposition, play an important part in the brain’s function and can it explain critical aspects of consciousness?[100]

Problems solved in the past 30 years #

[ edit]

General physics/quantum physics #

[ edit]

Cosmology and general relativity #

[ edit]

High-energy physics/particle physics #

[ edit]

  • Existence of pentaquarks (1964–2015): In July 2015, the LHCb collaboration at CERN identified pentaquarks in the Λ0
    b→J/ψK−p channel, which represents the decay of the bottom lambda baryon (Λ0
    b) into a J/ψ meson (J/ψ), a kaon (K−
    ) and a proton (p). The results showed that sometimes, instead of decaying directly into mesons and baryons, the Λ0
    b decayed via intermediate pentaquark states. The two states, named P+
    c(4380) and P+
    c(4450), had individual statistical significances of 9 σ and 12 σ, respectively, and a combined significance of 15 σ—enough to claim a formal discovery. The two pentaquark states were both observed decaying strongly to J/ψp, hence must have a valence quark content of two up quarks, a down quark, a charm quark, and an anti-charm quark (
    u

    u

    d

    c

    c
    ), making them charmonium-pentaquarks.[111]

  • Existence of quark-gluon plasma, a new phase of matter was discovered and confirmed in experiments at CERN- SPS (2000), BNL- RHIC (2005) and CERN- LHC (2010).[112]

  • Higgs boson and electroweak symmetry breaking (1963[113]–2012): The mechanism responsible for breaking the electroweak gauge symmetry, giving mass to the W and Z bosons, was solved with the discovery of the Higgs boson of the Standard Model, with the expected couplings to the weak bosons. No evidence of a strong dynamics solution, as proposed by technicolor, has been observed.

  • Origin of mass of most elementary particles: Solved with the discovery of the Higgs boson, which implies the existence of the Higgs field giving mass to these particles.

Astronomy and astrophysics #

[ edit]

Rapidly solved problems #

[ edit]

  1. ^ “This problem is widely regarded as one of the major obstacles to further progress in fundamental physics … Its importance has been emphasized by various authors from different aspects. For example, it has been described as a ‘veritable crisis” …] and even ’the mother of all physics problems’ … While it might be possible that people working on a particular problem tend to emphasize or even exaggerate its importance, those authors all agree that this is a problem that needs to be solved, although there is little agreement on what is the right direction to find the solution."[24]

  2. ^ When physicists strip neutrons from atomic nuclei, put them in a bottle, then count how many remain there after some time, they infer that neutrons radioactively decay in 14 minutes and 39 seconds, on average. But when other physicists generate beams of neutrons and tally the emerging protons — the particles that free neutrons decay into — they peg the average neutron lifetime at around 14 minutes and 48 seconds. The discrepancy between the “bottle” and “beam” measurements has persisted since both methods of gauging the neutron’s longevity began yielding results in the 1990s. At first, all the measurements were so imprecise that nobody worried. Gradually, though, both methods have improved, and still they disagree.[26]

  3. ^ Ginzburg, Vitaly L. (2001). The physics of a lifetime : reflections on the problems and personalities of 20th century physics. Berlin: Springer. pp.  3–200. ISBN  978-3-540-67534-1.

  4. ^ Hammond, Richard (1 May 2008). “The Unknown Universe: The Origin of the Universe, Quantum Gravity, Wormholes, and Other Things Science Still Can’t Explain”. Proceedings of the Royal Society of London, Series A. 456 (1999): 1685.

  5. ^ Womersley, J. (February 2005). “Beyond the Standard Model” (PDF). Symmetry Magazine. Archived from the original (PDF) on 17 October 2007. Retrieved 23 November 2010.

  6. ^ Overbye, Dennis (11 September 2023). “Don’t Expect a ‘Theory of Everything’ to Explain It All - Not even the most advanced physics can reveal everything we want to know about the history and future of the cosmos, or about ourselves”. The New York Times. Archived from the original on 11 September 2023. Retrieved 11 September 2023.

  7. ^ “Alcohol constrains physical constant in the early universe”. Phys Org. 13 December 2012. Archived from the original on 2 April 2015. Retrieved 25 March 2015.

  8. ^ Bagdonaite, J.; Jansen, P.; Henkel, C.; Bethlem, H. L.; Menten, K. M.; Ubachs, W. (13 December 2012). “A Stringent Limit on a Drifting Proton-to-Electron Mass Ratio from Alcohol in the Early Universe”. Science. 339 (6115): 46–48. Bibcode: 2013Sci…339…46B. doi: 10.1126/science.1224898. hdl: 1871/39591. PMID  23239626. S2CID  716087. Archived from the original on 17 January 2023. Retrieved 10 January 2020.

  9. ^ Sokal, Alan (22 July 1996). “Don’t Pull the String Yet on Superstring Theory”. New York Times. Archived from the original on 7 December 2008. Retrieved 17 February 2017.

  10. ^ Peres, Asher; Terno, Daniel R. (2004). “Quantum information and relativity theory”. Reviews of Modern Physics. 76 (1): 93–123. arXiv: quant-ph/0212023. Bibcode: 2004RvMP…76…93P. doi: 10.1103/revmodphys.76.93. S2CID  7481797.

  11. ^ Joshi, Pankaj S. (January 2009). “Do Naked Singularities Break the Rules of Physics?”. Scientific American. Archived from the original on 25 May 2012.

  12. ^ Harlow, Daniel (2018). “TASI Lectures on the Emergence of Bulk Physics in AdS/CFT”. Proceedings of Science. TASI2017: 002. doi: 10.22323/1.305.0002. hdl: 1721.1/121453.

  13. ^ Isham, C. J. (1993). “Canonical Quantum Gravity and the Problem of Time”. Integrable Systems, Quantum Groups, and Quantum Field Theories. NATO ASI Series. Springer, Dordrecht. pp. 157–287. arXiv: gr-qc/9210011. doi: 10.1007/978-94-011-1980-1_6. ISBN  9789401048743. S2CID  116947742.

  14. ^ “Yang-Mills & The Mass Gap”. Clay Mathematics Institute. Retrieved 9 April 2024.

  15. ^ Rees, Martin (3 May 2001). Just Six Numbers: The Deep Forces That Shape The Universe. New York, New York: Basic Books; First American edition. p. 4. ISBN  9780465036721.

  16. ^ Gribbin, J. and Rees, M., Cosmic Coincidences: Dark Matter, Mankind, and Anthropic Cosmology, pp. 7, 269. 1989, ISBN  0-553-34740-3

  17. ^ Davis, Paul (2007). Cosmic Jackpot: Why Our Universe Is Just Right for Life. New York: Orion Publications. p.  2. ISBN  978-0618592265.

  18. ^ Podolsky, Dmitry. “Top ten open problems in physics”. NEQNET. Archived from the original on 22 October 2012. Retrieved 24 January 2013.

  19. ^ Jump up to: a b c d e Brooks, Michael (19 March 2005). “13 things that do not make sense”. New Scientist. Issue 2491. Archived from the original on 23 June 2015. Retrieved 7 March 2011.

  20. ^ “Quanta Magazine”. Archived from the original on 27 April 2020. Retrieved 10 May 2020.

  21. ^ Jump up to: a b c d Abdalla, Elcio; AbellĂĄn, Guillermo Franco; Aboubrahim, Amin (11 March 2022). “Cosmology Intertwined: A Review of the Particle Physics, Astrophysics, and Cosmology Associated with the Cosmological Tensions and Anomalies”. Journal of High Energy Astrophysics. 34: 49. arXiv: 2203.06142v1. Bibcode: 2022JHEAp..34…49A. doi: 10.1016/j.jheap.2022.04.002. S2CID  247411131.

  22. ^ Krishnan, Chethan; Mohayaee, Roya; ColgĂĄin, Eoin Ó; Sheikh-Jabbari, M. M.; Yin, Lu (16 September 2021). “Does Hubble Tension Signal a Breakdown in FLRW Cosmology?”. Classical and Quantum Gravity. 38 (18): 184001. arXiv: 2105.09790. Bibcode: 2021CQGra..38r4001K. doi: 10.1088/1361-6382/ac1a81. ISSN  0264-9381. S2CID  234790314.

  23. ^ Jump up to: a b Ellis, G. F. R. (2009). “Dark energy and inhomogeneity”. Journal of Physics: Conference Series. 189 (1): 012011. Bibcode: 2009JPhCS.189a2011E. doi: 10.1088/1742-6596/189/1/012011. S2CID  250670331.

  24. ^ Jump up to: a b Colin, Jacques; Mohayaee, Roya; Rameez, Mohamed; Sarkar, Subir (20 November 2019). “Evidence for anisotropy of cosmic acceleration”. Astronomy and Astrophysics. 631: L13. arXiv: 1808.04597. Bibcode: 2019A&A…631L..13C. doi: 10.1051/0004-6361/201936373. S2CID  208175643. Archived from the original on 10 March 2022. Retrieved 25 March 2022.

  25. ^ Steinhardt, P. & Turok, N. (2006). “Why the Cosmological constant is so small and positive”. Science. 312 (5777): 1180–1183. arXiv: astro-ph/0605173. Bibcode: 2006Sci…312.1180S. doi: 10.1126/science.1126231. PMID  16675662. S2CID  14178620.

  26. ^ Jump up to: a b Wang, Qingdi; Zhu, Zhen; Unruh, William G. (11 May 2017). “How the huge energy of quantum vacuum gravitates to drive the slow accelerating expansion of the Universe”. Physical Review D. 95 (10): 103504. arXiv: 1703.00543. Bibcode: 2017PhRvD..95j3504W. doi: 10.1103/PhysRevD.95.103504. S2CID  119076077.

  27. ^ Dirac, Paul (1931). “Quantised singularities in the electromagnetic field” (PDF). Proceedings of the Royal Society A. 133 (821): 60. Bibcode: 1931RSPSA.133…60D. doi: 10.1098/rspa.1931.0130. Archived (PDF) from the original on 20 May 2011. Retrieved 25 December 2010.

  28. ^ Jump up to: a b Wolchover, Natalie (13 February 2018). “Neutron lifetime puzzle deepens, but no dark matter seen”. Quanta Magazine. Archived from the original on 30 July 2018. Retrieved 31 July 2018.

  29. ^ Li, Tianjun; Nanopoulos, Dimitri V.; Walker, Joel W. (2011). “Elements of fast proton decay”. Nuclear Physics B. 846 (1): 43–99. arXiv: 1003.2570. Bibcode: 2011NuPhB.846…43L. doi: 10.1016/j.nuclphysb.2010.12.014. S2CID  119246624.

  30. ^ Hansson, Johan (2010). “The “proton spin crisis” – a quantum query” (PDF). Progress in Physics. 3: 23. Archived from the original (PDF) on 4 May 2012. Retrieved 14 April 2012.

  31. ^ Langacker, Paul (2012). “Grand unification”. Scholarpedia. 7 (10): 11419. Bibcode: 2012SchpJ…711419L. doi: 10.4249/scholarpedia.11419.

  32. ^ Wu, T.-Y.; Hwang, W.-Y. Pauchy (1991). Relativistic Quantum Mechanics and Quantum Fields. World Scientific. ISBN  978-981-02-0608-6.

  33. ^ Blumhofer, A.; Hutter, M. (1997). “Family structure from periodic solutions of an improved gap equation”. Nuclear Physics. B484 (1): 80–96. Bibcode: 1997NuPhB.484…80B. CiteSeerX  10.1.1.343.783. doi: 10.1016/S0550-3213(96)00644-X.

  34. ^ “India-based Neutrino Observatory (INO)”. Tata Institute of Fundamental Research. Archived from the original on 26 April 2012. Retrieved 14 April 2012.

  35. ^ Nakamura, K.; et al. ( Particle Data Group) (2010). “2011 Review of Particle Physics”. J. Phys. G. 37 (7A): 075021. Bibcode: 2010JPhG…37g5021N. doi: 10.1088/0954-3899/37/7A/075021. hdl: 10481/34593. Archived from the original on 23 April 2012. Retrieved 25 April 2012.

  36. ^ Mention, G.; Fechner, M.; Lasserre, Th.; Mueller, Th.A.; Lhuillier, D.; Cribier, M.; Letourneau, A. (29 April 2011). “Reactor antineutrino anomaly”. Physical Review D. 83 (7): 073006. arXiv: 1101.2755. Bibcode: 2011PhRvD..83g3006M. doi: 10.1103/PhysRevD.83.073006. S2CID  14401655. Archived from the original on 17 January 2023. Retrieved 2 October 2021.

  37. ^ Fallot, Muriel (19 June 2017). “Getting to the bottom of an antineutrino anomaly”. Physics. 10: 66. Bibcode: 2017PhyOJ..10…66F. doi: 10.1103/Physics.10.66. Archived from the original on 2 October 2021. Retrieved 2 October 2021.

  38. ^ Blum, Thomas; Denig, Achim; Logashenko, Ivan; de Rafael, Eduardo; Roberts, B. Lee; Teubner, Thomas; Venanzoni, Graziano (2013). “The muon (g − 2) theory value: Present and future”. arXiv: 1311.2198 [ hep-ph].

  39. ^ Muir, H. (2 July 2003). “Pentaquark discovery confounds skeptics”. New Scientist. Archived from the original on 10 October 2008. Retrieved 8 January 2010.

  40. ^ Amit, G. (14 July 2015). “Pentaquark discovery at LHC shows long-sought new form of matter”. New Scientist. Archived from the original on 8 November 2020. Retrieved 14 July 2015.

  41. ^ Elliott, S. R.; Gavrin, V. N.; Haxton, W. C. (1 January 2024). “The gallium anomaly”. Progress in Particle and Nuclear Physics. 134: 104082. arXiv: 2306.03299. Bibcode: 2024PrPNP.13404082E. doi: 10.1016/j.ppnp.2023.104082. ISSN  0146-6410.

  42. ^ Michael J. Thompson (2014). “Grand Challenges in the Physics of the Sun and Sun-like Stars”. Frontiers in Astronomy and Space Sciences. 1: 1. arXiv: 1406.4228. Bibcode: 2014FrASS…1….1T. doi: 10.3389/fspas.2014.00001. S2CID  1547625.

  43. ^ Strohmayer, Tod E.; Mushotzky, Richard F. (20 March 2003). “Discovery of X-Ray Quasi-periodic Oscillations from an Ultraluminous X-Ray Source in M82: Evidence against Beaming”. The Astrophysical Journal. 586 (1): L61–L64. arXiv: astro-ph/0303665. Bibcode: 2003ApJ…586L..61S. doi: 10.1086/374732. S2CID  118992703.

  44. ^ Titarchuk, Lev; Fiorito, Ralph (10 September 2004). “Spectral Index and Quasi-Periodic Oscillation Frequency Correlation in Black Hole Sources: Observational Evidence of Two Phases and Phase Transition in Black Holes” (PDF). The Astrophysical Journal. 612 (2): 988–999. arXiv: astro-ph/0405360. Bibcode: 2004ApJ…612..988T. doi: 10.1086/422573. hdl: 2060/20040182332. S2CID  4689535. Archived from the original (PDF) on 3 February 2014. Retrieved 25 January 2013.

  45. ^ Shoji Kato (2012). “An Attempt to Describe Frequency Correlations among kHz QPOs and HBOs by Two-Armed Nearly Vertical Oscillations”. Publications of the Astronomical Society of Japan. 64 (3): 62. arXiv: 1202.0121. Bibcode: 2012PASJ…64…62K. doi: 10.1093/pasj/64.3.62. S2CID  118498018.

  46. ^ Sarre, Peter J. (2006). “The diffuse interstellar bands: A major problem in astronomical spectroscopy”. Journal of Molecular Spectroscopy. 238 (1): 1. arXiv: astro-ph/0608113. Bibcode: 2006JMoSp.238….1S. doi: 10.1016/j.jms.2006.03.009.

  47. ^ Cami, Jan; Cox, Nick L. J.; Farhang, Amin; Smoker, Jonathan; Elyajouri, Meriem; Lallement, Rosine; Bacalla, Xavier; Bhatt, Neil H.; Bron, Emeric; Cordiner, Martin A.; de Koter, Alex; Ehrenfreund, Pascale; Evans, Chris; Foing, Bernard; Javadi, Atefeh; Joblin, Christine; Kaper, Lex; Khosroshahi, Habib G.; Laverick, Mike; Le Petit, Franck; Linnartz, Harold; Marshall, Charlotte C. M.; Monreal-Ibero, Ana; Mulas, Giacomo; Roueff, Evelyne; Royer, Pierre; Salama, Farid; Sarre, Peter J.; Smith, Keith T.; Spaans, Marco; van Loon, Jacco T.; Wade, Gregg (2018). “The ESO Diffuse Interstellar Band Large Exploration Survey (EDIBLES)” (PDF). The Messenger. 171. European Southern Observatory: 31. Bibcode: 2018Msngr.171…31C. doi: 10.18727/0722-6691/5066.

  48. ^ Ferrarese, Laura; Merritt, David (2000). “A Fundamental Relation between Supermassive Black Holes and their Host Galaxies”. The Astrophysical Journal. 539 (1): L9–L12. arXiv: astro-ph/0006053. Bibcode: 2000ApJ…539L…9F. doi: 10.1086/312838. S2CID  6508110.

  49. ^ Jump up to: a b c d e f Baez, John C. (March 2006). “Open Questions in Physics”. Usenet Physics FAQ. University of California, Riverside: Department of Mathematics. Archived from the original on 4 June 2011. Retrieved 7 March 2011.

  50. ^ “Scientists Find That Saturn’s Rotation Period is a Puzzle”. NASA. 28 June 2004. Archived from the original on 29 August 2011. Retrieved 22 March 2007.

  51. ^ Condon, J. J.; Cotton, W. D.; Greisen, E. W.; Yin, Q. F.; Perley, R. A.; Taylor, G. B.; Broderick, J. J. (1998). “The NRAO VLA Sky Survey”. The Astronomical Journal. 115 (5): 1693–1716. Bibcode: 1998AJ….115.1693C. doi: 10.1086/300337. S2CID  120464396.

  52. ^ Singal, Ashok K. (2011). “Large peculiar motion of the solar system from the dipole anisotropy in sky brightness due to distant radio sources”. The Astrophysical Journal. 742 (2): L23–L27. arXiv: 1110.6260. Bibcode: 2011ApJ…742L..23S. doi: 10.1088/2041-8205/742/2/L23. S2CID  119117071.

  53. ^ Tiwari, Prabhakar; Kothari, Rahul; Naskar, Abhishek; Nadkarni-Ghosh, Sharvari; Jain, Pankaj (2015). “Dipole anisotropy in sky brightness and source count distribution in radio NVSS data”. Astroparticle Physics. 61: 1–11. arXiv: 1307.1947. Bibcode: 2015APh….61….1T. doi: 10.1016/j.astropartphys.2014.06.004. S2CID  119203300.

  54. ^ Tiwari, P.; Jain, P. (2015). “Dipole anisotropy in integrated linearly polarized flux density in NVSS data”. Monthly Notices of the Royal Astronomical Society. 447 (3): 2658–2670. arXiv: 1308.3970. Bibcode: 2015MNRAS.447.2658T. doi: 10.1093/mnras/stu2535. S2CID  118610706.

  55. ^ Hutsemekers, D. (1998). “Evidence for very large-scale coherent orientations of quasar polarization vectors” (PDF). Astronomy and Astrophysics. 332: 410–428. Bibcode: 1998A&A…332..410H.

  56. ^ HutsemĂ©kers, D.; Lamy, H. (2001). “Confirmation of the existence of coherent orientations of quasar polarization vectors on cosmological scales”. Astronomy & Astrophysics. 367 (2): 381–387. arXiv: astro-ph/0012182. Bibcode: 2001A&A…367..381H. doi: 10.1051/0004-6361:20000443. S2CID  17157567.

  57. ^ Jain, P.; Narain, G.; Sarala, S. (2004). “Large-scale alignment of optical polarizations from distant QSOs using coordinate-invariant statistics”. Monthly Notices of the Royal Astronomical Society. 347 (2): 394–402. arXiv: astro-ph/0301530. Bibcode: 2004MNRAS.347..394J. doi: 10.1111/j.1365-2966.2004.07169.x. S2CID  14190653.

  58. ^ Angelica de Oliveira-Costa; Tegmark, Max; Zaldarriaga, Matias; Hamilton, Andrew (2004). “The significance of the largest scale CMB fluctuations in WMAP”. Physical Review D. 69 (6): 063516. arXiv: astro-ph/0307282. Bibcode: 2004PhRvD..69f3516D. doi: 10.1103/PhysRevD.69.063516. S2CID  119463060.

  59. ^ Eriksen, H. K.; Hansen, F. K.; Banday, A. J.; GĂłrski, K. M.; Lilje, P. B. (2004). “Asymmetries in the Cosmic Microwave Background Anisotropy Field”. The Astrophysical Journal. 605 (1): 14–20. arXiv: astro-ph/0307507. Bibcode: 2004ApJ…605…14E. doi: 10.1086/382267. S2CID  15696508.

  60. ^ Pramoda Kumar Samal; Saha, Rajib; Jain, Pankaj; Ralston, John P. (2008). “Testing Isotropy of Cosmic Microwave Background Radiation”. Monthly Notices of the Royal Astronomical Society. 385 (4): 1718–1728. arXiv: 0708.2816. Bibcode: 2008MNRAS.385.1718S. doi: 10.1111/j.1365-2966.2008.12960.x. S2CID  988092.

  61. ^ Pramoda Kumar Samal; Saha, Rajib; Jain, Pankaj; Ralston, John P. (2009). “Signals of Statistical Anisotropy in WMAP Foreground-Cleaned Maps”. Monthly Notices of the Royal Astronomical Society. 396 (511): 511–522. arXiv: 0811.1639. Bibcode: 2009MNRAS.396..511S. doi: 10.1111/j.1365-2966.2009.14728.x. S2CID  16250321.

  62. ^ Casagrande, L.; Schönrich, R.; Asplund, M.; Cassisi, S.; RamĂ­rez, I.; MelĂ©ndez, J.; Bensby, T.; Feltzing, S. (2011). “New constraints on the chemical evolution of the solar neighbourhood and Galactic disc(s)”. Astronomy & Astrophysics. 530: A138. arXiv: 1103.4651. Bibcode: 2011A&A…530A.138C. doi: 10.1051/0004-6361/201016276. S2CID  56118016.

  63. ^ Bensby, T.; Feltzing, S.; Lundström, I. (July 2004). “A possible age–metallicity relation in the Galactic thick disk?”. Astronomy and Astrophysics. 421 (3): 969–976. arXiv: astro-ph/0403591. Bibcode: 2004A&A…421..969B. doi: 10.1051/0004-6361:20035957. S2CID  10469794.

  64. ^ Gilmore, G.; Asiri, H. M. (2011). “Open Issues in the Evolution of the Galactic Disks”. Stellar Clusters & Associations: A RIA Workshop on Gaia. Proceedings. Granada: 280. Bibcode: 2011sca..conf..280G.

  65. ^ Casagrande, L.; Silva Aguirre, V.; Schlesinger, K. J.; Stello, D.; Huber, D.; Serenelli, A. M.; Scho Nrich, R.; Cassisi, S.; Pietrinferni, A.; Hodgkin, S.; Milone, A. P.; Feltzing, S.; Asplund, M. (2015). “Measuring the vertical age structure of the Galactic disc using asteroseismology and SAGA”. Monthly Notices of the Royal Astronomical Society. 455 (1): 987–1007. arXiv: 1510.01376. Bibcode: 2016MNRAS.455..987C. doi: 10.1093/mnras/stv2320. S2CID  119113283.

  66. ^ Fields, Brian D. (2012). “The Primordial Lithium Problem”. Annual Review of Nuclear and Particle Science. 61 (2011): 47–68. arXiv: 1203.3551. Bibcode: 2011ARNPS..61…47F. doi: 10.1146/annurev-nucl-102010-130445. S2CID  119265528.

  67. ^ Platts, E.; Weltman, A.; Walters, A.; Tendulkar, S.P.; Gordin, J.E.B.; Kandhai, S. (2019). “A living theory catalogue for fast radio bursts”. Physics Reports. 821: 1–27. arXiv: 1810.05836. Bibcode: 2019PhR…821….1P. doi: 10.1016/j.physrep.2019.06.003. S2CID  119091423.

  68. ^ Charles Fefferman. “Existence and Uniqueness of the Navier-Stokes Equation” (PDF). Clay Mathematics Institute. Archived (PDF) from the original on 14 November 2020. Retrieved 29 April 2021.

  69. ^ Aranson, Igor S.; Tsimring, Lev S. (1 June 2006). “Patterns and collective behavior in granular media: Theoretical concepts”. Reviews of Modern Physics. 78 (2): 641–692. arXiv: cond-mat/0507419. doi: 10.1103/RevModPhys.78.641. Yet despite major efforts by many groups, the theoretical description of granular systems remains largely a plethora of different, often contradictory concepts and approaches.

  70. ^ Schlein, Benjamin. “Graduate Seminar on Partial Differential Equations in the Sciences – Energy and Dynamics of Boson Systems”. Hausdorff Center for Mathematics. Archived from the original on 4 May 2013. Retrieved 23 April 2012.

  71. ^ Kenneth Chang (29 July 2008). “The Nature of Glass Remains Anything but Clear”. The New York Times. Archived from the original on 14 September 2017. Retrieved 17 February 2017.

  72. ^ P.W. Anderson (1995). “Through the Glass Lightly”. Science. 267 (5204): 1615–1616. doi: 10.1126/science.267.5204.1615-e. PMID  17808155. S2CID  28052338. The deepest and most interesting unsolved problem in solid state theory is probably the theory of the nature of glass and the glass transition.

  73. ^ Zaccone, A. (2023). Theory of Disordered Solids. Lecture Notes in Physics. Vol. 1015 (1st ed.). Springer. doi: 10.1007/978-3-031-24706-4. ISBN  978-3-031-24705-7. S2CID  259299183.

  74. ^ Pohl, R.O.; etc, etc (2002). “Low-temperature thermal conductivity and acoustic attenuation in amorphous solids”. Rev. Mod. Phys. 74: 991. doi: 10.1080/14786437208229210.

  75. ^ Leggett, A.J. (1991). “Amorphous materials at low temperatures: why are they so similar?”. Physica B. 169 (1–4): 322–327. Bibcode: 1991PhyB..169..322L. doi: 10.1016/0921-4526(91)90246-B.

  76. ^ Cryogenic electron emission phenomenon has no known physics explanation Archived 5 June 2011 at the Wayback Machine. Physorg.com. Retrieved on 20 October 2011.

  77. ^ Meyer, H. O. (1 March 2010). “Spontaneous electron emission from a cold surface”. Europhysics Letters. 89 (5): 58001. Bibcode: 2010EL…..8958001M. doi: 10.1209/0295-5075/89/58001. S2CID  122528463. Archived from the original on 20 February 2020. Retrieved 20 April 2018.

  78. ^ Storey, B. D.; Szeri, A. J. (8 July 2000). “Water vapour, sonoluminescence and sonochemistry”. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 456 (1999): 1685–1709. Bibcode: 2000RSPSA.456.1685S. doi: 10.1098/rspa.2000.0582. S2CID  55030028.

  79. ^ Wu, C. C.; Roberts, P. H. (9 May 1994). “A Model of Sonoluminescence”. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 445 (1924): 323–349. Bibcode: 1994RSPSA.445..323W. doi: 10.1098/rspa.1994.0064. S2CID  122823755.

  80. ^ Yoshida, Beni (1 October 2011). “Feasibility of self-correcting quantum memory and thermal stability of topological order”. Annals of Physics. 326 (10): 2566–2633. arXiv: 1103.1885. Bibcode: 2011AnPhy.326.2566Y. doi: 10.1016/j.aop.2011.06.001. ISSN  0003-4916. S2CID  119611494.

  81. ^ Dean, Cory R. (2015). “Even denominators in odd places”. Nature Physics. 11 (4): 298–299. Bibcode: 2015NatPh..11..298D. doi: 10.1038/nphys3298. ISSN  1745-2481. S2CID  123159205.

  82. ^ Mukherjee, Prabir K. (1998). “Landau Theory of Nematic-Smectic-A Transition in a Liquid Crystal Mixture”. Molecular Crystals & Liquid Crystals. 312 (1): 157–164. Bibcode: 1998MCLCA.312..157M. doi: 10.1080/10587259808042438.

  83. ^ A. Yethiraj, “Recent Experimental Developments at the Nematic to Smectic-A Liquid Crystal Phase Transition” Archived 15 May 2013 at the Wayback Machine, Thermotropic Liquid Crystals: Recent Advances, ed. A. Ramamoorthy, Springer 2007, chapter 8.

  84. ^ Norris, David J. (2003). “The Problem Swept Under the Rug”. In Klimov, Victor (ed.). Electronic Structure in Semiconductors Nanocrystals: Optical Experiment (in Semiconductor and Metal Nanocrystals: Synthesis and Electronic and Optical Properties_)_. CRC Press. p. 97. ISBN  978-0-203-91326-0. Archived from the original on 27 April 2022. Retrieved 18 October 2020.

  85. ^ Lipa, J. A.; Nissen, J. A.; Stricker, D. A.; Swanson, D. R.; Chui, T. C. P. (14 November 2003). “Specific heat of liquid helium in zero gravity very near the lambda point”. Physical Review B. 68 (17): 174518. arXiv: cond-mat/0310163. Bibcode: 2003PhRvB..68q4518L. doi: 10.1103/PhysRevB.68.174518. S2CID  55646571.

  86. ^ Campostrini, Massimo; Hasenbusch, Martin; Pelissetto, Andrea; Vicari, Ettore (6 October 2006). “Theoretical estimates of the critical exponents of the superfluid transition in $^{4}\mathrm{He}$ by lattice methods”. Physical Review B. 74 (14): 144506. arXiv: cond-mat/0605083. doi: 10.1103/PhysRevB.74.144506. S2CID  118924734.

  87. ^ Hasenbusch, Martin (26 December 2019). “Monte Carlo study of an improved clock model in three dimensions”. Physical Review B. 100 (22): 224517. arXiv: 1910.05916. Bibcode: 2019PhRvB.100v4517H. doi: 10.1103/PhysRevB.100.224517. ISSN  2469-9950. S2CID  204509042.

  88. ^ Chester, Shai M.; Landry, Walter; Liu, Junyu; Poland, David; Simmons-Duffin, David; Su, Ning; Vichi, Alessandro (2020). “Carving out OPE space and precise $O(2)$ model critical exponents”. Journal of High Energy Physics. 2020 (6): 142. arXiv: 1912.03324. Bibcode: 2020JHEP…06..142C. doi: 10.1007/JHEP06(2020)142. S2CID  208910721.

  89. ^ Rychkov, Slava (31 January 2020). “Conformal bootstrap and the λ-point specific heat experimental anomaly”. Journal Club for Condensed Matter Physics. doi: 10.36471/JCCM_January_2020_02. Archived from the original on 9 June 2020. Retrieved 8 February 2020.

  90. ^ Barton, G.; Scharnhorst, K. (1993). “QED between parallel mirrors: light signals faster than c, or amplified by the vacuum”. Journal of Physics A. 26 (8): 2037. Bibcode: 1993JPhA…26.2037B. doi: 10.1088/0305-4470/26/8/024. A more recent follow-up paper is Scharnhorst, K. (1998). “The velocities of light in modified QED vacua”. Annalen der Physik. 7 (7–8): 700–709. arXiv: hep-th/9810221. Bibcode: 1998AnP…510..700S. doi: 10.1002/(SICI)1521-3889(199812)7:7/8<700::AID-ANDP700>3.0.CO;2-K. S2CID  120489943.

  91. ^ Jump up to: a b c Aaronson, Scott. “Ten Semi-Grand Challenges for Quantum Computing Theory”. ScottAaronson.com. Retrieved 1 September 2023.

  92. ^ Ball, Phillip (2021). “Major Quantum Computing Strategy Suffers Serious Setbacks”. Quanta Magazine. Retrieved 2 September 2023.

  93. ^ Skyrme, Tess (20 March 2023). “The Status of Room-Temperature Quantum Computers”. EE Times Europe. Retrieved 1 September 2023.

  94. ^ Shor, Peter (2000). “Quantum Information Theory: Results and Open Problems” (PDF). In Alon N.; Bourgain J.; Connes A.; Gromov M.; Milman V. (eds.). Visions in Mathematics, GAFA 2000 Special Volume: Part II. Modern BirkhĂ€user Classics. BirkhĂ€user Basel. pp. 816–838. doi: 10.1007/978-3-0346-0425-3_9. ISBN  978-3-0346-0425-3.

  95. ^ F. Wagner (2007). “A quarter-century of H-mode studies” (PDF). Plasma Physics and Controlled Fusion. 49 (12B): B1. Bibcode: 2007PPCF…49….1W. doi: 10.1088/0741-3335/49/12B/S01. S2CID  498401. Archived from the original (PDF) on 23 February 2019..

  96. ^ AndrĂ© Balogh; Rudolf A. Treumann (2013). “Section 7.4 The Injection Problem”. Physics of Collisionless Shocks: Space Plasma Shock Waves. Springer. p. 362. ISBN  978-1-4614-6099-2. Archived from the original on 17 January 2023. Retrieved 3 September 2015.

  97. ^ Goldstein, Melvyn L. (2001). “Major Unsolved Problems in Space Plasma Physics”. Astrophysics and Space Science. 277 (1/2): 349–369. Bibcode: 2001Ap&SS.277..349G. doi: 10.1023/A:1012264131485. S2CID  189821322.

  98. ^ Dill, K. A.; MacCallum, J. L. (2012). “The Protein-Folding Problem, 50 Years On”. Science. 338 (6110): 1042–1046. Bibcode: 2012Sci…338.1042D. doi: 10.1126/science.1219021. ISSN  0036-8075. PMID  23180855. S2CID  5756068.

  99. ^ Cabello, AdĂĄn (2017). “Interpretations of quantum theory: A map of madness”. In Lombardi, Olimpia; Fortin, Sebastian; Holik, Federico; LĂłpez, Cristian (eds.). What is Quantum Information?. Cambridge University Press. pp. 138–143. arXiv: 1509.04711. Bibcode: 2015arXiv150904711C. doi: 10.1017/9781316494233.009. ISBN  9781107142114. S2CID  118419619.

  100. ^ Wiseman, Howard (2014). “The Two Bell’s Theorems of John Bell”. Journal of Physics A: Mathematical and Theoretical. 47 (42): 424001. arXiv: 1402.0351. Bibcode: 2014JPhA…47P4001W. doi: 10.1088/1751-8113/47/42/424001. ISSN  1751-8121. S2CID  119234957.

  101. ^ Fuchs, Christopher A.; Mermin, N. David; Schack, RĂŒdiger (2014). “An introduction to QBism with an application to the locality of quantum mechanics”. American Journal of Physics. 82 (8): 749. arXiv: 1311.5253. Bibcode: 2014AmJPh..82..749F. doi: 10.1119/1.4874855. S2CID  56387090.

  102. ^ Atmanspacher, Harald (2020), “Quantum Approaches to Consciousness”, in Zalta, Edward N. (ed.), The Stanford Encyclopedia of Philosophy (Summer 2020 ed.), Metaphysics Research Lab, Stanford University, retrieved 12 April 2023

  103. ^ Philip M. Pearle (1970), “Hidden-Variable Example Based upon Data Rejection”, Phys. Rev. D, 2 (8): 1418–1425, Bibcode: 1970PhRvD…2.1418P, doi: 10.1103/PhysRevD.2.1418

  104. ^ Hensen, B.; et al. (21 October 2015). “Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres”. Nature. 526 (7575): 682–686. arXiv: 1508.05949. Bibcode: 2015Natur.526..682H. doi: 10.1038/nature15759. PMID  26503041. S2CID  205246446.

  105. ^ Markoff, Jack (21 October 2015). “Sorry, Einstein. Quantum Study Suggests ‘Spooky Action’ Is Real”. New York Times. Archived from the original on 31 July 2019. Retrieved 21 October 2015.

  106. ^ Giustina, M.; et al. (16 December 2015). “Significant-Loophole-Free Test of Bell’s Theorem with Entangled Photons”. Physical Review Letters. 115 (25): 250401. arXiv: 1511.03190. Bibcode: 2015PhRvL.115y0401G. doi: 10.1103/PhysRevLett.115.250401. PMID  26722905. S2CID  13789503.

  107. ^ Shalm, L. K.; et al. (16 December 2015). “Strong Loophole-Free Test of Local Realism”. Physical Review Letters. 115 (25): 250402. arXiv: 1511.03189. Bibcode: 2015PhRvL.115y0402S. doi: 10.1103/PhysRevLett.115.250402. PMC  5815856. PMID  26722906.

  108. ^ “Einstein papers at the Instituut-Lorentz”. Archived from the original on 19 May 2015. Retrieved 30 April 2016.

  109. ^ Castelvecchi, Davide; Witze, Witze (11 February 2016). “Einstein’s gravitational waves found at last”. Nature News. doi: 10.1038/nature.2016.19361. S2CID  182916902. Archived from the original on 24 December 2018. Retrieved 11 February 2016.

  110. ^ B. P. Abbott; et al. (LIGO Scientific Collaboration and Virgo Collaboration) (2016). “Observation of Gravitational Waves from a Binary Black Hole Merger”. Physical Review Letters. 116 (6): 061102. arXiv: 1602.03837. Bibcode: 2016PhRvL.116f1102A. doi: 10.1103/PhysRevLett.116.061102. PMID  26918975. S2CID  124959784.

  111. ^ “Gravitational waves detected 100 years after Einstein’s prediction”. www.nsf.gov. National Science Foundation. Archived from the original on 19 June 2020. Retrieved 11 February 2016.

  112. ^ Pretorius, Frans (2005). “Evolution of Binary Black-Hole Spacetimes”. Physical Review Letters. 95 (12): 121101. arXiv: gr-qc/0507014. Bibcode: 2005PhRvL..95l1101P. doi: 10.1103/PhysRevLett.95.121101. PMID  16197061. S2CID  24225193. Campanelli, M.; Lousto, C. O.; Marronetti, P.; Zlochower, Y. (2006). “Accurate Evolutions of Orbiting Black-Hole Binaries without Excision”. Physical Review Letters. 96 (11): 111101. arXiv: gr-qc/0511048. Bibcode: 2006PhRvL..96k1101C. doi: 10.1103/PhysRevLett.96.111101. PMID  16605808. S2CID  5954627. Baker, John G.; Centrella, Joan; Choi, Dae-Il; Koppitz, Michael; Van Meter, James (2006). “Gravitational-Wave Extraction from an Inspiraling Configuration of Merging Black Holes”. Physical Review Letters. 96 (11): 111102. arXiv: gr-qc/0511103. Bibcode: 2006PhRvL..96k1102B. doi: 10.1103/PhysRevLett.96.111102. PMID  16605809. S2CID  23409406.

  113. ^ R. Aaij et al. ( LHCb collaboration) (2015). “Observation of J/ψp resonances consistent with pentaquark states in Λ0
    b→J/ψK−p decays”. Physical Review Letters. 115 (7): 072001. arXiv: 1507.03414. Bibcode: 2015PhRvL.115g2001A. doi: 10.1103/PhysRevLett.115.072001. PMID  26317714. S2CID  119204136.

  114. ^ Rafelski, Johann (2020). “Discovery of Quark-Gluon Plasma: Strangeness Diaries”. The European Physical Journal Special Topics. 229 (1): 1–140. arXiv: 1911.00831. Bibcode: 2020EPJST.229….1R. doi: 10.1140/epjst/e2019-900263-x. ISSN  1951-6355.

  115. ^ Higgs, Peter (24 November 2010). “My Life as a Boson” (PDF). Talk given by Peter Higgs at King’s College, London, 24 November 2010, expanding on a paper originally presented in 2001. Archived from the original (PDF) on 1 May 2014. Retrieved 17 January 2013. – the original 2001 paper can be found at: Duff and Liu, ed. (2003) [year of publication]. 2001 A Spacetime Odyssey: Proceedings of the Inaugural Conference of the Michigan Center for Theoretical Physics, Michigan, USA, 21–25 May 2001. World Scientific. pp. 86–88. ISBN  978-9812382313. Archived from the original on 27 April 2022. Retrieved 17 January 2013.

  116. ^ Jump up to: a b Kouveliotou, Chryssa; Meegan, Charles A.; Fishman, Gerald J.; Bhat, Narayana P.; Briggs, Michael S.; Koshut, Thomas M.; Paciesas, William S.; Pendleton, Geoffrey N. (1993). “Identification of two classes of gamma-ray bursts”. The Astrophysical Journal. 413: L101. Bibcode: 1993ApJ…413L.101K. doi: 10.1086/186969.

  117. ^ Cho, Adrian (16 October 2017). “Merging neutron stars generate gravitational waves and a celestial light show”. Science. Archived from the original on 30 October 2021. Retrieved 16 October 2017.

  118. ^ Casttelvecchi, Davide (25 August 2017). “Rumours swell over new kind of gravitational-wave sighting”. Nature News. doi: 10.1038/nature.2017.22482. Archived from the original on 16 October 2017. Retrieved 27 August 2017.

  119. ^ Shull, J. Michael, Britton D. Smith, and Charles W. Danforth. “The baryon census in a multiphase intergalactic medium: 30% of the baryons may still be missing.” The Astrophysical Journal 759.1 (2012): 23.

  120. ^ “Half the universe’s missing matter has just been finally found”. New Scientist. Archived from the original on 13 October 2017. Retrieved 12 October 2017.

  121. ^ Nicastro, F.; Kaastra, J.; Krongold, Y.; Borgani, S.; Branchini, E.; Cen, R.; Dadina, M.; Danforth, C. W.; Elvis, M.; Fiore, F.; Gupta, A.; Mathur, S.; Mayya, D.; Paerels, F.; Piro, L.; Rosa-Gonzalez, D.; Schaye, J.; Shull, J. M.; Torres-Zafra, J.; Wijers, N.; Zappacosta, L. (June 2018). “Observations of the missing baryons in the warm–hot intergalactic medium”. Nature. 558 (7710): 406–409. arXiv: 1806.08395. Bibcode: 2018Natur.558..406N. doi: 10.1038/s41586-018-0204-1. ISSN  0028-0836. PMID  29925969. S2CID  49347964.

  122. ^ Cleveland, Bruce T.; Daily, Timothy; Davis, Jr., Raymond; Distel, James R.; Lande, Kenneth; Lee, C. K.; Wildenhain, Paul S.; Ullman, Jack (1998). “Measurement of the Solar Electron Neutrino Flux with the Homestake Chlorine Detector”. The Astrophysical Journal. 496 (1): 505–526. Bibcode: 1998ApJ…496..505C. doi: 10.1086/305343.

  123. ^ Helled, Ravit; Galanti, Eli; Kaspi, Yohai (2015). “Saturn’s fast spin determined from its gravitational field and oblateness”. Nature. 520 (7546): 202–204. arXiv: 1504.02561. Bibcode: 2015Natur.520..202H. doi: 10.1038/nature14278. PMID  25807487. S2CID  4468877.

  124. ^ Wilczek, Frank (2012). “Quantum Time Crystals”. Physical Review Letters. 109 (16): 160401. arXiv: 1202.2539. Bibcode: 2012PhRvL.109p0401W. doi: 10.1103/PhysRevLett.109.160401. ISSN  0031-9007. PMID  23215056. S2CID  1312256.

  125. ^ Shapere, Alfred; Wilczek, Frank (2012). “Classical Time Crystals”. Physical Review Letters. 109 (16): 160402. arXiv: 1202.2537. Bibcode: 2012PhRvL.109p0402S. doi: 10.1103/PhysRevLett.109.160402. ISSN  0031-9007. PMID  23215057. S2CID  4506464.

  126. ^ Khemani, Vedika; Lazarides, Achilleas; Moessner, Roderich; Sondhi, S. L. (21 June 2016). “Phase Structure of Driven Quantum Systems”. Physical Review Letters. 116 (25): 250401. arXiv: 1508.03344. Bibcode: 2016PhRvL.116y0401K. doi: 10.1103/PhysRevLett.116.250401. PMID  27391704. S2CID  883197.

  127. ^ Else, Dominic V.; Bauer, Bela; Nayak, Chetan (25 August 2016). “Floquet Time Crystals”. Physical Review Letters. 117 (9): 090402. arXiv: 1603.08001. Bibcode: 2016PhRvL.117i0402E. doi: 10.1103/PhysRevLett.117.090402. PMID  27610834. S2CID  1652633.

  128. ^ Yao, N. Y.; Potter, A. C.; Potirniche, I.-D.; Vishwanath, A. (2017). “Discrete Time Crystals: Rigidity, Criticality, and Realizations”. Physical Review Letters. 118 (3): 030401. arXiv: 1608.02589. Bibcode: 2017PhRvL.118c0401Y. doi: 10.1103/PhysRevLett.118.030401. ISSN  0031-9007. PMID  28157355. S2CID  206284432. Archived from the original on 24 June 2021. Retrieved 21 November 2021.

  129. ^ Zhang, J.; et al. (8 March 2017). “Observation of a discrete time crystal”. Nature. 543 (7644): 217–220. arXiv: 1609.08684. Bibcode: 2017Natur.543..217Z. doi: 10.1038/nature21413. PMID  28277505. S2CID  4450646.

  130. ^ Choi, S.; et al. (8 March 2017). “Observation of discrete time-crystalline order in a disordered dipolar many-body system”. Nature. 543 (7644): 221–225. arXiv: 1610.08057. Bibcode: 2017Natur.543..221C. doi: 10.1038/nature21426. PMC  5349499. PMID  28277511.

  131. ^ Khaire, V.; Srianand, R. (2015). “Photon underproduction crisis: Are QSOs sufficient to resolve it?”. Monthly Notices of the Royal Astronomical Society: Letters. 451: L30–L34. arXiv: 1503.07168. Bibcode: 2015MNRAS.451L..30K. doi: 10.1093/mnrasl/slv060. S2CID  119263441.

  132. ^ Van Leeuwen, Floor (1999). “HIPPARCOS distance calibrations for 9 open clusters”. Astronomy and Astrophysics. 341: L71. Bibcode: 1999A&A…341L..71V.

  133. ^ Charles Francis; Erik Anderson (2012). “XHIP-II: Clusters and associations”. Astronomy Letters. 38 (11): 681–693. arXiv: 1203.4945. Bibcode: 2012AstL…38..681F. doi: 10.1134/S1063773712110023. S2CID  119285733.

  134. ^ OPERA collaboration (12 July 2012). “Measurement of the neutrino velocity with the OPERA detector in the CNGS beam”. Journal of High Energy Physics. 2012 (10): 93. arXiv: 1109.4897. Bibcode: 2012JHEP…10..093A. doi: 10.1007/JHEP10(2012)093. S2CID  17652398.

  135. ^ Turyshev, S.; Toth, V.; Kinsella, G.; Lee, S. C.; Lok, S.; Ellis, J. (2012). “Support for the Thermal Origin of the Pioneer Anomaly”. Physical Review Letters. 108 (24): 241101. arXiv: 1204.2507. Bibcode: 2012PhRvL.108x1101T. doi: 10.1103/PhysRevLett.108.241101. PMID  23004253. S2CID  2368665.

  136. ^ Overbye, Dennis (23 July 2012). “Mystery Tug on Spacecraft Is Einstein’s ‘I Told You So’”. The New York Times. Archived from the original on 27 August 2017. Retrieved 24 January 2014.

Backlinks

  • No backlinks found

Interactive Graph